ボラティリティーとは？

オプションのプレミアムは、本質的価値と時間価値を合わせた価格だったよね。

うん。　なんとなく分かったような。

本質的価値は、コール・オプションの場合は原資産の価格から権利行使価格を引いた額、プット・オプションの場合は権利行使価格から原資産の価格を引いた額になる。

つまり、オプションの本質的価値は、原資産価格と権利行使価格によって決まる。

イン・ザ・マネーのオプションだけが本質的価値を持ってるんだよね。

うん、そうだったね。
では、時間価値はどうやって決まるんだろう？

えっと、オプションの満期日までの期間が長ければ長いほど時間価値が上がるんでしょ？

そのとおり。
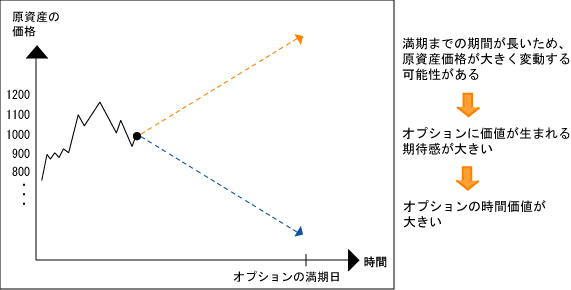
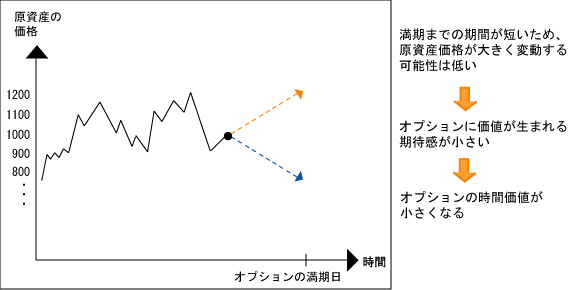
しかし、実はもう一つ、時間価値を決める重要な要素があるんだ。
その要素のことを「ボラティリティ（Volatility)」というよ。

ぼらてぃりてぃ？？

そう。　ボラティリティ。
ボラティリティの仕組みについては、どんなものなのか「ざっくり」覚えておけばOKだ。

これから先の説明も、完璧に覚える必要はないからね。
大事なのは、実際のトレードにどう役立つか、ということだから。

オプションのプレミアムは、以下の要素によって決定される。

上記のうち、最初の２つが本質的価値を決め、残り３つが時間価値に影響する。

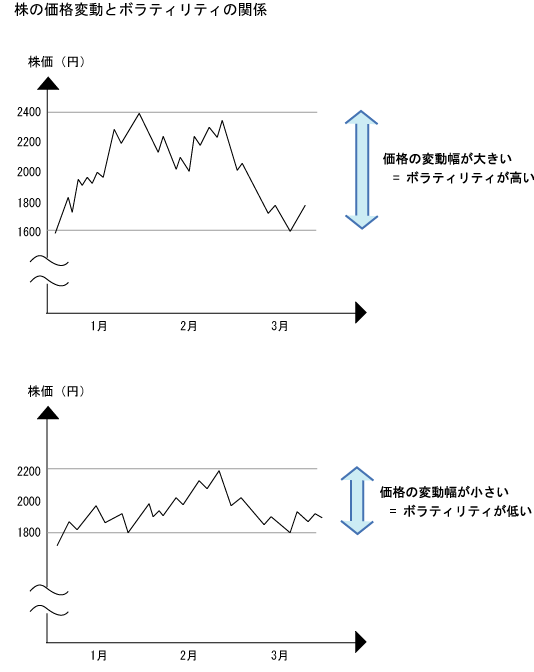
ボラティリティとは、価格の変動幅の比率という意味だよ。
ボラティリティは、価格変動が大きければ高くなり、価格変動が小さくなれば低くなる。

う～ん…
このボラティリティというのが、どうしてオプションの価格に関わってくるのかピンと来ないんだけど…

オプションの買い手と売り手の立場に立って考えると分かりやすいかも知れない。
たとえば、原資産の価格変動が大きいオプションと、原資産の価格変動が小さいオプションの場合、買い手にとってどっちが有利だろうか？

オプションの買い手は、原資産が逆方向に大きく動いたとしても損失は限定…
もし良い方向に大きく動けば、たくさんの利益を上げられるんだよね。

でも原資産の価格が少ししか動かないと、たとえ良い方向に価格が動いたとしてもイン・ザ・マネーにならない可能性がある…。

そっか！　ということは、買い手にとっては原資産の価格変動が大きい、つまりボラティリティが高いオプションの方が、価値が大きい（=価格が高くなる）ということ？

そういうこと！
逆に、ボラティリティが低いオプションは、買い手にとって価値が小さい（=価格が安くなる）ということになる。

ボラティリティが高い	オプションのプレミアムが高くなる
ボラティリティが低い	オプションのプレミアムが低くなる

ボラティリティには、ヒストリカル・ボラティリティとインプライド・ボラティリティの2種類があるんだ。

ひすとらりぃ…　横文字が多すぎて心が折れそう。

むむぅ。　確かに舌を噛みそうになるけど、違いは覚えて置いた方がいいよ。
実際にオプションを取引する時には、必ず出てくる言葉だしね。

りょーかい。　ベスト・エフォート型で覚えとくよ。

回線業者の言い訳みたいだな。

ではまず、ヒストリカル・ボラティリティ。
長いので、「HV」と略されることが多い。

HVは、過去の価格変動率を平均化することによって算出される。 上で説明したボラティリティも、正確にはHVのことだよ。

下記のチャートは、日経平均株価とそのHVを示している。 日経平均株価の変動によって、HVが継続的に変化しているのが分かる。

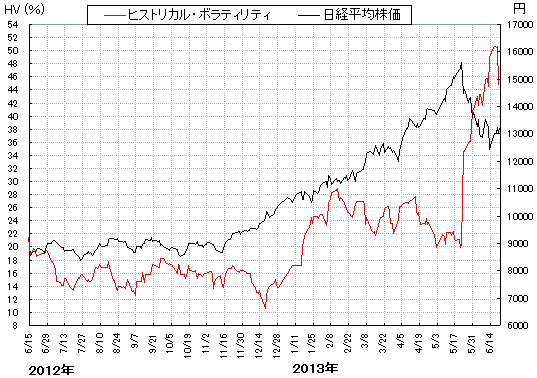
日経平均が大きく変動したときに、ボラティリティが上昇しているね。

そうだね。　それがHVの特徴だよ。

そしてオプションで活用されるもう１つのボラティリティが、インプライド・ボラティリティだ。 こちらは略して「IV」と呼ばれる。

HVが、過去の（原資産の）継続的な価格変動を元に算出されるのに対して、IVは市場で取引されているオプション価格から算出される。

オプショントレードでは、このIVが重要な意味を持つ。

具体的にはどうやって計算されるの？

まず前提として、オプションの理論価格という考え方を理解する必要がある。
理論価格というのは、「このオプションは、だいたいこれくらいの価格で取引されるはず」というのを、計算式で求めたものだ。

具体的には、原資産価格、権利行使価格、満期までの時間、金利、そしてヒストリカル・ボラティリティ（HV）を計算式に当てはめることで、オプションの理論価格を求めることができる。

ただ、実際に取引されているオプションの価格は、必ずしも理論価格とは一致しない。 あくまで、マーケットの他の要素から推測される「理論上」の参考価格みたいなものだ。

次に、上で使った計算式を応用して、「ヒストリカル・ボラティリティ」の値を取り除く。
そして、プレミアムの理論値の代わりに、実際に取引されているオプションのプレミアムを代入する。

そうすると、ある日時においてボラティリティ以外の要素（オプションのプレミアム、原資産価格、権利行使価格、満期までの時間、金利）は全て確定するから、その時点での「ボラティリティの実測値」を逆算によって求めることができるんだ。

こうして計算したものを、オプションのインプライド・ボラティリティ（IV）と呼んでいるんだよ。
HVが、過去の原資産価格の変動から計算される数値であるのに対して、IVは実際に市場で取引されているオプションの値段（プレミアム）から計算されるボラティリティだ。

IVは、原資産価格が今後どれくらい大きく（小さく）変動しそうかということについて、市場のオプショントレーダーがどう見ているかを表す数値とも言える。

トレーダーが原資産価格の大きな変動を予想しているときは、オプションのプレミアムが高くなり、その結果IVも高くなる。
逆に、原資産相場がそれほど変動しないと思われているときには、オプションのプレミアムが低下し、IVも低くなる。

HVが純粋な統計データであるのに対して、IVは相場の先行きに対する投資家心理を示す数値とも言えるね。

またオプションの売買戦略においては、IVの高低により、相対的に割高なオプションを売り、割安なオプションを買うといった判断が行われる。

ほほぉー。
過去の統計がHV。 投資家の今後の見通しがIVと。

で、実際の取引でIVとかって見られるの？

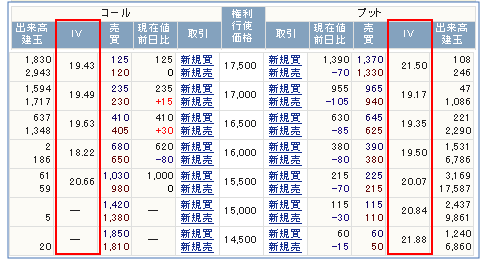
証券会社によっては、実際にオプションを取引する際に、下のような画面でIVを参照することができるよ。

ほんとだ。
実際の取引でも、IVが出てくるんだね。
それにしても、今まで株とかやってて、ボラティリティなんて聞いたことも無かったよ。

株式投資でも、機関投資家などの大口トレーダーは、ボラティリティを考慮してリスク管理をしているみたいだね。
でも、個人投資家にとってはそれほど馴染みがあるものでもない。

一方、オプションは「原資産の価格がどれくらい動くか？」ということが非常に重要な意味を持つ投資商品だから、個人投資家にとってもボラティリティは無視できないんだ。

なるほどね。
ややこしいけど、頑張って覚えておくか。

うむ。 仕組みを大まかに覚えておけば、ボラティリティを利用したオプション戦略なども理解しやすくなるはずだ。

では次回は、ボラティリティを実際の取引に役立てる方法を解説しよう。